Data Science. Bayes Theorem

#data-science

Many engineers haven't had direct exposure to statistics or Data Science. Yet, when building data pipelines or translating Data Scientist prototypes into robust, maintainable code, engineering complexities often arise. For Data/ML engineers and new Data Scientists, I've put together this series of posts.

I'll explain core Data Science approaches in simple terms, building from basic concepts to more complex ones.

The whole series:

Bayes' theorem is one of the core concepts in probability theory and a crucial tool in Data Science. It lets us update our beliefs as new evidence becomes available — an essential mechanism when dealing with real-world uncertainties.

Intuitive Understanding

Imagine a man sitting with his back to a perfectly flat, square table. He asks his assistant to throw a ball onto the table. With no prior knowledge of where the ball landed, it could be anywhere on that table. However, he wants to pinpoint its location analytically, without simply turning around to look.

To do this, he asks the assistant to throw another ball onto the table and note whether it lands to the left, right, front, or back of the first ball. He jots down the result, and then he asks for more and more throws, gathering clues with each new ball thrown.

With each piece of information, he refines his understanding of where that first ball could be. He'll never know with complete certainty, but he can shrink the uncertainty over time, updating his belief with each new observation.

And that's how Thomas Bayes saw the world. His thinking wasn't about proving absolute truths but about honing our beliefs through evidence. This idea forms the crux of Bayesian inference — a concept foundational to both science and statistics.

Practical Explanation

Let's break it down with two overlapping events, A and B. Imagine event A represents "I get wet today" and event B represents "it will rain today". These events are interdependent, with one often influencing the probability of the other.

To calculate the probability of A given that B has happened (i.e., the likelihood of getting wet if it's raining), we focus on the shaded overlap in the Venn diagram, representing A ∩ B.

A ∩ B

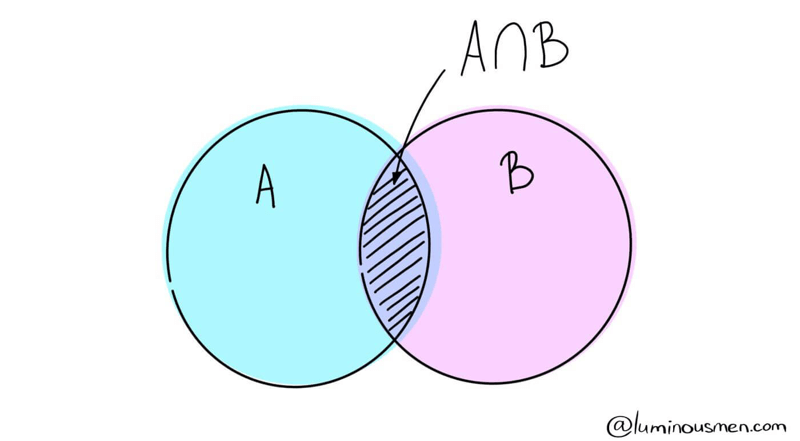
Here's how it looks mathematically:

$$ P(A|B) = \frac{P(A ∩ B)}{P(B + A ∩ B)} $$

Since B has occurred, we're only concerned with the part of A that overlaps with B. Thus, the probability of A given B is:

$$ P(A|B) = \frac{P(A ∩ B)}{P(B)} $$

Similarly, we can express B given A as:

$$ P(B|A) = \frac{P(A ∩ B)}{P(A)} $$

Now, rearrange to reveal the final Bayes' theorem formula:

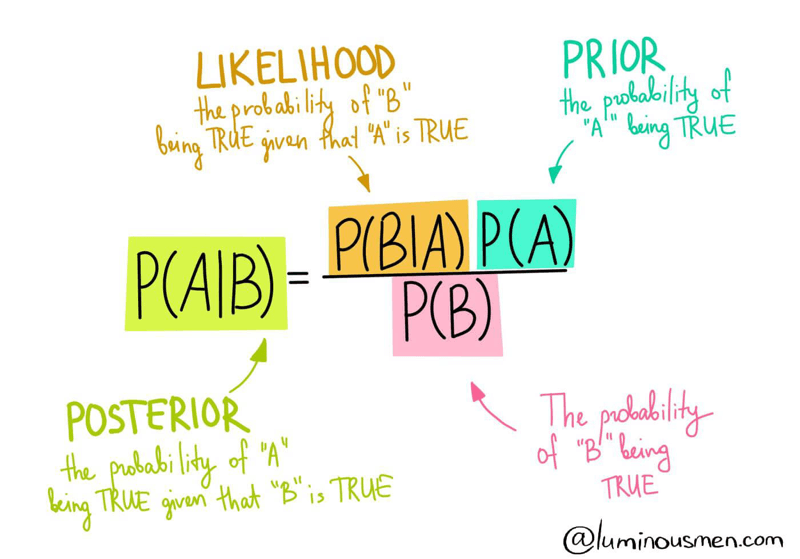
Bayes' theorem

In this formula:

$#P(A|B)#$: Posterior probability - the probability of A given B has occurred
$#P(B|A)#$: Likelihood - the probability of B given A
$#P(A), P(B)#$: Prior probabilities of events A and B occurring independently

It's worth noting that for independent events, $#P(B | A) = P(B)#$. This means if A does not influence B, knowing A occurred doesn't change B's probability.

Example:

Imagine drawing a single card from a standard deck of 52 cards. The probability of pulling a king is 4/52, as there are four kings in the deck. We'll call this initial probability P(King).

Now, let's say we gain new information: someone glances at the card and sees that it's a face card. This allows us to calculate the updated probability $#P(King|Face)#$, using Bayes' theorem:

$$ P(King|Face) = \frac{P(Face|King) * P(King)}{P(Face)} $$

Since every king is also a face card, we have $#P(Face|King) = 1#$. There are 12 face cards in total, so $#P(Face) = 12/52#$.

Plugging in these values:

$$ P(\text{King}|\text{Face}) = \frac{1 \cdot \frac{4}{52}}{\frac{12}{52}} = \frac{4}{12} = \frac{1}{3} $$

This shows how Bayes' theorem lets us update our probability with additional evidence, refining our understanding with each new piece of information.

For those wanting to play with Bayes' theorem interactively, check out this calculator:

Conclusion

The essence of Bayesian inference is in gradually becoming "less wrong" with each new data point. Our initial belief, or prior, is simply our best guess without extra information. With more data, we adjust this prior, making our conclusions progressively more accurate.

Interestingly, people often emphasize the posterior probability without enough consideration for the prior probability. But the prior is vital — it's our starting point. Without a reasonable prior, the posterior is misleading.

Through this simple formula, Bayes' theorem has given us a powerful tool in data science, enabling everything from A/B testing to machine learning models. But don't rush — master the basics first, and the advanced applications will fall into place.